数据结构与算法(6): 树形结构-AVL树

发表于   |   分类于

介绍

AVL树是根据它的发明者Adelson-Velsky和Landis命名的。

  AVL树是带有平衡条件的二叉查找树。这个平衡条件必须要容易保持，而且保证树的深度必须是$O(\log{N})$，所以AVL树的查找、插入和删除在平均和最坏情况下都是$O(\log{N})$。
它的特点是AVL树中任何节点的两个子树的高度最大差别为1。

节点定义

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
private static class AvlNode<T> {
        T element;
        AvlNode<T> left;
        AvlNode<T> right;
        int height;
        public AvlNode(T element) {
            this(element, null, null);
        }
        public AvlNode(T element, AvlNode<T> left, AvlNode<T> right) {
            this.element = element;
            this.left = left;
            this.right = right;
            this.height = 1;
        }
    }

恢复平衡

  当发生插入或删除操作时，就有可能破坏AVL树的平衡条件，所以为了恢复平衡需要对树进行简单的修正，也就是旋转。
 旋转分为4种状态两种情况，如下图：
 1. 插入发生在“外边”的情况（即左-左或右-右的情况），该情况通过树的一次单旋转完成调整。
 2. 插入发生在“内部”的情况（即左-右或右-左的情况），该情况通过复杂些的双旋转完成调整。

左左（LL） 旋转

如下图，左边是旋转之前的树，右边是旋转之后的树。从中可以发现，经过一次旋转又变成了AVL树。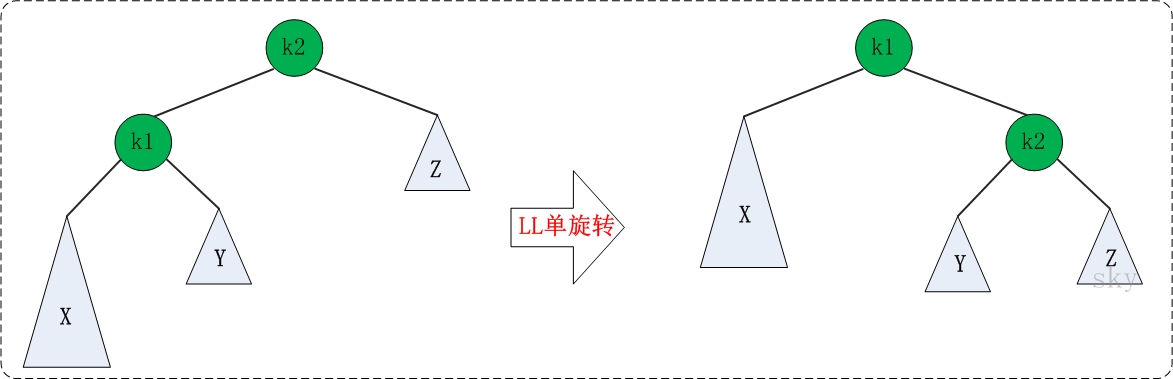

对于LL旋转，你可以这样理解为：LL旋转是围绕”失去平衡的AVL根节点”进行的，也就是节点k2；而且由于是LL情况，即左左情况，就用手抓着”左孩子，即k1”使劲摇。将k1变成根节点，k2变成k1的右子树，”k1的右子树”变成”k2的左子树”。

1
2
3
4
5
6
7
8
9
10
11
12
13
/**
 * 左左 单旋转
 * @param k2 平衡条件破坏的子树的根节点
 * @return 返回新的根节点
 */
private AvlNode<T> rotateWithLeftChild(AvlNode<T> k2) {
    AvlNode<T> k1 = k2.left;
    k2.left = k1.right;
    k1.right = k2;
    k2.height = Math.max(height(k2.left), height(k2.right)) + 1;
    k1.height = Math.max(height(k1.left), height(k1.right)) + 1;
    return k1;
}

右右（LL） 旋转

RR是与LL对称的情况，如下图，也是经过一次旋转又变成了AVL树。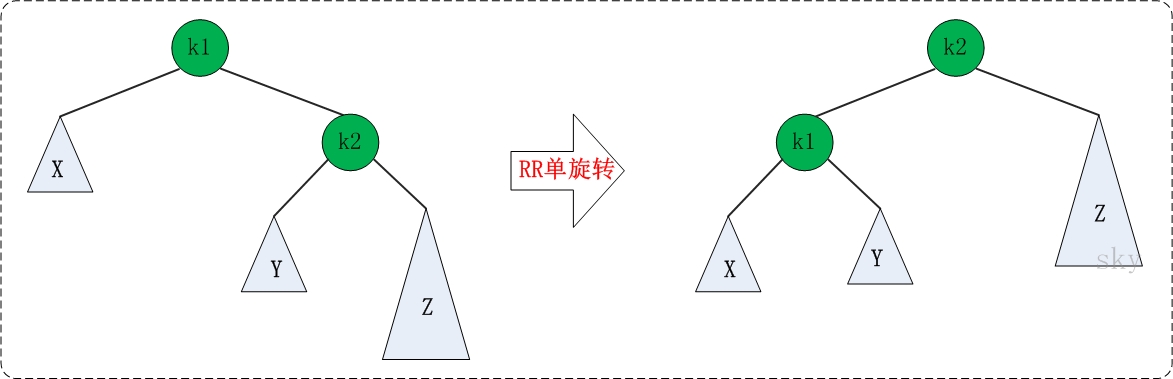

1
2
3
4
5
6
7
8
9
10
11
12
13
/**
  * 右右 单旋转
  * @param k2 平衡条件破坏的子树的根节点
  * @return 返回新的根节点
  */
 private AvlNode<T> rotateWithRightChild(AvlNode<T> k2) {
     AvlNode<T> k1 = k2.right;
     k2.right = k1.left;
     k1.left = k2;
     k2.height = Math.max(height(k2.left), height(k2.right)) + 1;
     k1.height = Math.max(height(k1.left), height(k1.right)) + 1;
     return k1;
 }

左右（LR） 旋转

LR失去平衡的情况，需要经过两次旋转才能让AVL树恢复平衡。

第一次旋转是围绕”k1”进行的”RR旋转”，第二次是围绕”k3”进行的”LL旋转”。

1
2
3
4
5
6
7
8
9
10
/**
  * 左右 双旋转
  * 先进行一次右旋转, 在进行一次左旋转
  * @param k3 平衡条件破坏的子树的根节点
  * @return 返回新的根节点
  */
 private AvlNode<T> doubleRotateWithLeftChild(AvlNode<T> k3) {
     k3.left = rotateWithRightChild(k3.left);
     return rotateWithLeftChild(k3);
 }

右左（RL） 旋转

RL是与LR的对称情况！RL恢复平衡的旋转方法如下图。

第一次旋转是围绕”k3”进行的”LL旋转”，第二次是围绕”k1”进行的”RR旋转”。

1
2
3
4
5
6
7
8
9
10
/**
 * 右左 双旋转
 * 先进行一次左旋转, 在进行一次右旋转
 * @param k3 平衡条件破坏的子树的根节点
 * @return 返回新的根节点
 */
private AvlNode<T> doubleRotateWithRightChild(AvlNode<T> k3) {
    k3.right = rotateWithLeftChild(k3.right);
    return rotateWithRightChild(k3);
}

完整实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
/**
 * AVL树
 */
public class AvlTree<T extends Comparable<? super T>> {
    private AvlNode<T> root;
    private static class AvlNode<T> {
        T element;
        AvlNode<T> left;
        AvlNode<T> right;
        int height;
        public AvlNode(T element) {
            this(element, null, null);
        }
        public AvlNode(T element, AvlNode<T> left, AvlNode<T> right) {
            this.element = element;
            this.left = left;
            this.right = right;
            this.height = 1;
        }
    }
    /**
     * 插入元素到Avl树
     * @param ele
     */
    public void insert(T ele){
        root = insert(ele, root);
    }
    /**
     * 插入元素到子树中
     * @param ele
     * @param subroot 子树根节点
     * @return 新的子树根节点
     */
    private AvlNode<T> insert(T ele, AvlNode<T> subroot){
        if (subroot == null){
            return new AvlNode<T>(ele);
        }
        int cmpResult = ele.compareTo(subroot.element);
        if (cmpResult < 0){
            subroot.left = insert(ele, subroot.left);
            // 往左插入元素时, 破坏平衡条件
            if (height(subroot.left) - height(subroot.right) == 2){
                // 判断是左左还是左右情况
                if (subroot.left.element.compareTo(ele) > 0){
                    subroot = rotateWithLeftChild(subroot);
                }else {
                    subroot = doubleRotateWithLeftChild(subroot);
                }
            }
        }else if (cmpResult > 0){
            subroot.right = insert(ele, subroot.right);
            // 往右插入元素时, 破坏平衡条件
            if (height(subroot.right) - height(subroot.left) == 2){
                // 判断是右右还是右左情况
                if (subroot.right.element.compareTo(ele) < 0){
                    subroot = rotateWithRightChild(subroot);
                }else {
                    subroot = doubleRotateWithRightChild(subroot);
                }
            }
        }else {
            // Duplicate; do nothing
        }
        // 更新subroot的height
        subroot.height = Math.max(height(subroot.left), height(subroot.right)) + 1;
        return subroot;
    }
    /**
     * 从Avl树种删除元素
     * @param ele
     */
    public void remove(T ele){
        root = remove(ele, root);
    }
    /**
     * 从Avl子树中删除元素
     * @param ele
     * @param subroot 子树根节点
     * @return 新的子树根节点
     */
    private AvlNode<T> remove(T ele, AvlNode<T> subroot){
        if (subroot == null){
            return null;
        }
        int cmpResult = ele.compareTo(subroot.element);
        if (cmpResult < 0){
            subroot.left = remove(ele, subroot.left);
            if (height(subroot.right) - height(subroot.left) == 2){
                // 删除左子树的节点失去平衡
                if (height(subroot.right.left) > height(subroot.right.right)){
                    subroot = doubleRotateWithRightChild(subroot);
                }else {
                    subroot = rotateWithRightChild(subroot);
                }
            }
        }else if (cmpResult > 0){
            subroot.right = remove(ele, subroot.right);
            if (height(subroot.left) - height(subroot.right) == 2){
                // 删除右子树的节点失去平衡
                if (height(subroot.left.right) > height(subroot.left.left)){
                    subroot = doubleRotateWithLeftChild(subroot);
                }else {
                    subroot = rotateWithLeftChild(subroot);
                }
            }
        }else {
            // 对应删除的节点
            if (subroot.left != null && subroot.right != null){
                // 左右子树都非空
                if (height(subroot.left) > height(subroot.right)){
                    // 如果左子树比右子树高
                    // 1、找出tree的左子树的最大节点
                    // 2、将该最大节点赋给tree
                    // 3、从tree的左子树删除该最大节点
                    // 这种方式的好处：删除tree的左子树最大节点后, AVL树仍然是平衡的
                    AvlNode<T> leftMax = maximum(subroot.left);
                    subroot.element = leftMax.element;
                    subroot.left = remove(leftMax.element, subroot.left);
                }else {
                    // 如果右子树比左子树高或相等
                    // 1、找出tree的右子树的最小节点
                    // 2、将该最小节点赋给tree
                    // 3、从tree的右子树删除该最小节点
                    // 这种方式的好处：删除tree的右子树最小节点后, AVL树仍然是平衡的
                    AvlNode<T> rightMin = minimum(subroot.right);
                    subroot.element = rightMin.element;
                    subroot.right = remove(rightMin.element, subroot.right);
                }
            }else {
                subroot = (subroot.left != null) ? subroot.left : subroot.right;
            }
        }
        return subroot;
    }
    /**
     * 左左 单旋转
     * @param k2 平衡条件破坏的子树的根节点
     * @return 返回新的根节点
     */
    private AvlNode<T> rotateWithLeftChild(AvlNode<T> k2) {
        AvlNode<T> k1 = k2.left;
        k2.left = k1.right;
        k1.right = k2;
        k2.height = Math.max(height(k2.left), height(k2.right)) + 1;
        k1.height = Math.max(height(k1.left), height(k1.right)) + 1;
        return k1;
    }
    /**
     * 右右 单旋转
     * @param k2 平衡条件破坏的子树的根节点
     * @return 返回新的根节点
     */
    private AvlNode<T> rotateWithRightChild(AvlNode<T> k2) {
        AvlNode<T> k1 = k2.right;
        k2.right = k1.left;
        k1.left = k2;
        k2.height = Math.max(height(k2.left), height(k2.right)) + 1;
        k1.height = Math.max(height(k1.left), height(k1.right)) + 1;
        return k1;
    }
    /**
     * 左右 双旋转
     * 先进行一次右旋转, 在进行一次左旋转
     * @param k3 平衡条件破坏的子树的根节点
     * @return 返回新的根节点
     */
    private AvlNode<T> doubleRotateWithLeftChild(AvlNode<T> k3) {
        k3.left = rotateWithRightChild(k3.left);
        return rotateWithLeftChild(k3);
    }
    /**
     * 右左 双旋转
     * 先进行一次左旋转, 在进行一次右旋转
     * @param k3 平衡条件破坏的子树的根节点
     * @return 返回新的根节点
     */
    private AvlNode<T> doubleRotateWithRightChild(AvlNode<T> k3) {
        k3.right = rotateWithLeftChild(k3.right);
        return rotateWithRightChild(k3);
    }
    private int height(AvlNode<T> node) {
        return node == null ? 0 : node.height;
    }
    /**
     * 查找该子树的最大节点
     * @param subroot
     * @return
     */
    private AvlNode<T> maximum(AvlNode<T> subroot){
        if (subroot == null){
            return null;
        }
        while (subroot.right != null){
            subroot = subroot.right;
        }
        return subroot;
    }
    /**
     * 查找该子树的最小节点
     * @param subroot
     * @return
     */
    public AvlNode<T> minimum(AvlNode<T> subroot){
        if (subroot == null){
            return null;
        }
        while (subroot.left != null){
            subroot = subroot.left;
        }
        return subroot;
    }
    public void print(){
        if (root != null){
            print(root, root.element, 0);
        }
    }
    /**
     * @param node 打印的节点
     * @param ele ele 父节点的值
     * @param direction 0:根节点;-1:父节点的左儿子节点;1:父节点的右儿子节点
     */
    private void print(AvlNode<T> node, T ele, int direction){
        if (node != null){
            if (direction == 0){
                System.out.printf("%s是根节点\n", ele);
            }else {
                System.out.printf("%s是%s的%s儿子节点\n", node.element, ele, direction==-1?"left":"right");
            }
            print(node.left, node.element, -1);
            print(node.right, node.element, 1);
        }
    }
}

注：本文内容引自http://www.cnblogs.com/skywang12345/p/3577479.html