数据结构与算法(7): 树形结构-伸展树

发表于   |   分类于

介绍

伸展树（Splay Tree）和AVL树一样是一种特殊的二叉查找树。

  特点: 当某个节点被访问时，伸展树会通过旋转使该节点成为树根。这样做的好处是，下次要访问该节点时，能够迅速的访问到该节点。
  伸展树保证从空树开始连续M次对树的操作最多花费O($M*\log{N}$)时间，但不排除任意单次操作花费O(N)时间的可能。伸展树基于这样的事实：对于二叉查找树来说，每次操作最坏情形时间O(N)并不坏，只要相对不常发生就行。

伸展splaying

自底向上伸展

  伸展树主要有三种旋转操作：单旋转，一字形旋转和之字形旋转。

zig形

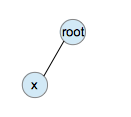
zig：当目标节点x是根节点的左子节点或右子节点时，进行一次单旋转，将目标节点调整到根节点的位置。

zig-zag形

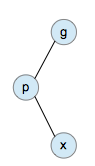
zig-zag：当目标节点X、父节点P和祖父节G点成”zig-zag”构型时，进行一次双旋转，将目标节点调整到祖父节点的位置。从祖父节点开始进行两次异向的单旋转操作。

zig-zig形

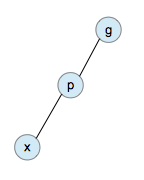
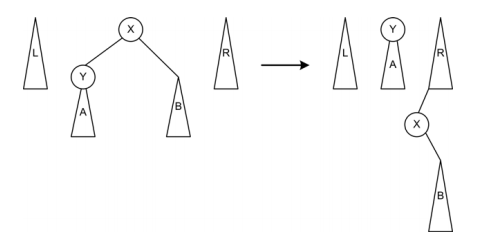
zig-zig：当目标节点X、父节点P和祖父节点G成”zig-zig”构型时，进行一次zig-zig操作，将目标节点调整到祖父节点的位置。从祖父节点开始进行两次同向的单旋转操作。

注：Bottom-up splay trees are hard to implement. (Sad Story)

自顶向下伸展

  在自底向上的伸展树中，我们需要求一个节点的父节点和祖父节点，因此这种伸展树难以实现。因此，我们可以构建自顶向下的伸展树。
  当我们沿着树向下搜索某个节点X的时候，我们将搜索路径上的节点及其子树移走。我们构建两棵临时的树──左树和右树。没有被移走的节点构成的树称作中树。

  • 左树：包含所有已经知道比目标节点小的节点。
  • 右树：包含所有已经知道比目标节点大的节点。
  • 中树：没有被移走的节点。

zig形

孩子即为要查找的点，只需要一次连接操作。

zig-zag形

孙子为要查找的点，而且呈之字形，只需要两次连接操作。

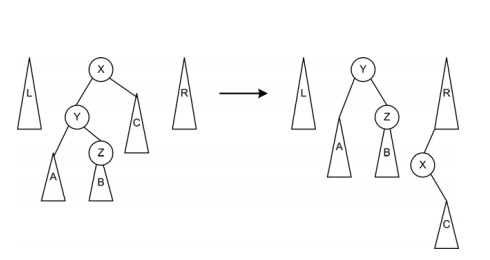
zig-zig形

孙子为要查找的点，而且呈一字形，先要进行一次旋转操作，再进行一次连接操作。

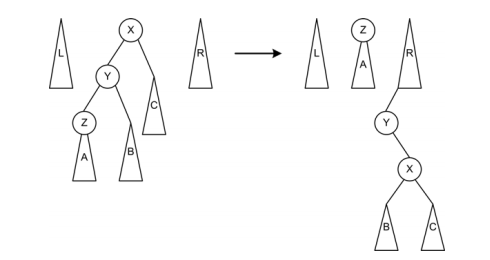
合并

将中树的左右子树分别连接到左树的右子树和右树的左子树上。将左右树作为X的左右子树。

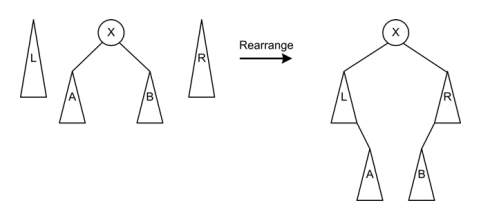
TopDown实现

伸展splay

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
/**
    * 自顶向下伸展
    * 构建两棵临时的树──左树和右树。没有被移走的节点构成的树称作中树。
    * 1、目标节点和root相连时：一次link操作完成伸展
    * 2、目标节点有父节点和祖先节点, 并且呈之字形：通过两次link操作完成伸展
    * 3、目标节点有父节点和祖先节点, 并且呈一字形：先通过一次旋转, 再通过一次link操作完成伸展 (这里不是很懂，如果也通过两次link操作也能达到把目标节点移动到root的目的啊????)
    * 注意此处的节点N, 最后所有的左树集中在N的右子树上, 而所有的右树集中在N的左子树上。
    * 因为每次left link需要将中树上的部分节点移到左树的最右端(也就是最大的位置上), 这里的节点l的作用可以看做是为了方便在左树的最右端继续添加从中树移过来的节点;
    * 同理, right link时, 节点r和节点l的作用类似。
    * @param ele
    * @param tree
    * @return
    */
   private SplayNode<T> topDownSplay(T ele, SplayNode<T> tree){
       if (tree == null){
           return null;
       }
       SplayNode<T> N = new SplayNode<T>();
       SplayNode<T> l = N;
       SplayNode<T> r = N;
       SplayNode<T> c;
       for (;;){
           int cmpResult = ele.compareTo(tree.element);
           if (cmpResult < 0){
               if (tree.left == null){
                   break;
               }
               /* rotate right*/
               if (ele.compareTo(tree.left.element) < 0){
                   c = tree.left;
                   tree.left = c.right;
                   c.right = tree;
                   tree = c;
                   if (tree.left == null){
                       break;
                   }
               }
               /* link right */
               r.left = tree;
               r = tree;
               tree = tree.left;
           }else if (cmpResult > 0){
               if (tree.right == null){
                   break;
               }
               /* rotate left */
               if (ele.compareTo(tree.right.element) > 0){
                   c = tree.right;
                   tree.right = c.left;
                   c.left = tree;
                   tree = c;
                   if (tree.right == null){
                       break;
                   }
               }
               /* link left */
               l.right = tree;
               l = tree;
               tree = tree.right;
           }else {
               break;
           }
       }
       /* assemble */
       l.right = tree.left;
       r.left = tree.right;
       tree.left = N.right;
       tree.right = N.left;
       return tree;
   }
   
   /**
    * 伸展
    * @param ele
    * @return
    */
   public SplayNode<T> splay(T ele){
       return topDownSplay(ele, root);
   }

插入insert

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/**
    * @param ele
    * @param node
    * @return 返回子树node的新的根节点
    */
   private SplayNode<T> insert(T ele, SplayNode<T> node) {
       if (node == null) {
           return new SplayNode<T>(ele);
       }
       int cmpResult = ele.compareTo(node.element);
       if (cmpResult < 0) {
           node.left = insert(ele, node.left);
       } else if (cmpResult > 0) {
           node.right = insert(ele, node.right);
       } else {
           // 插入的元素重复
           System.out.println("INFO: duplicated element");
       }
       return node;
   }
   
   /**
    * 插入
    * @param ele
    */
   public void insert(T ele){
       root = insert(ele, root);
       root = splay(ele);
   }

删除remove

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/**
    * 1、首先对ele进行一次伸展
    * 2、然后判断移动到根节点的元素是不是ele
    *    2.1、如果相等, 则找到该元素ele的前驱节点作为新的根节点
    *    2.2、如果不等, 则不做处理, 因为一开始的伸展操作就已经将ele的前驱节点移动到根节点了
    * @param ele
    * @return
    */
   private SplayNode<T> remove(T ele, SplayNode<T> tree){
       if (tree == null){
           return null;
       }
       tree = topDownSplay(ele, tree);
       if (tree.element.compareTo(ele) == 0){
           // 找到该元素, 对树进行调整并删除该元素
           SplayNode<T> x;
           if (tree.left != null){
               // 删除该元素后, 需要重新伸展树得到一个根节点
               // 从左子树中找到最大的节点(删除元素的前驱节点)作为新的根节点
               tree.left = topDownSplay(ele, tree.left);
               // 此时左子树不存在右儿子, 将原树的右子树直接赋给伸展后的左子树的右儿子
               tree.left.right = tree.right;
               tree = tree.left;
           }else {
               tree = tree.right;
           }
       }
       return tree;
   }
public void remove(T ele){
       root = remove(ele, root);
   }

完整实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
    /**
     * 伸展树
     */
    public class SplayTree<T extends Comparable<? super T>> {
    private SplayNode<T> root;
    private static class SplayNode<T>{
        private T element;
        SplayNode<T> left;
        SplayNode<T> right;
        public SplayNode() {
            this.left = null;
            this.right = null;
        }
        public SplayNode(T element) {
            this(element, null, null);
        }
        public SplayNode(T element, SplayNode<T> left, SplayNode<T> right) {
            this.element = element;
            this.left = left;
            this.right = right;
        }
    }
    /**
     * 插入
     * @param ele
     */
    public void insert(T ele){
        root = insert(ele, root);
        root = splay(ele);
    }
    /**
     * @param ele
     * @param node
     * @return 返回子树node的新的根节点
     */
    private SplayNode<T> insert(T ele, SplayNode<T> node) {
        if (node == null) {
            return new SplayNode<T>(ele);
        }
        int cmpResult = ele.compareTo(node.element);
        if (cmpResult < 0) {
            node.left = insert(ele, node.left);
        } else if (cmpResult > 0) {
            node.right = insert(ele, node.right);
        } else {
            // 插入的元素重复
            System.out.println("INFO: duplicated element");
        }
        return node;
    }
    /**
     * 删除元素
     * @param ele
     */
    public void remove(T ele){
        root = remove(ele, root);
    }
    /**
     * 1、首先对ele进行一次伸展
     * 2、然后判断移动到根节点的元素是不是ele
     *    2.1、如果相等, 则找到该元素ele的前驱节点作为新的根节点
     *    2.2、如果不等, 则不做处理, 因为一开始的伸展操作就已经将ele的前驱节点移动到根节点了
     * @param ele
     * @return
     */
    private SplayNode<T> remove(T ele, SplayNode<T> tree){
        if (tree == null){
            return null;
        }
        tree = topDownSplay(ele, tree);
        if (tree.element.compareTo(ele) == 0){
            // 找到该元素, 对树进行调整并删除该元素
            SplayNode<T> x;
            if (tree.left != null){
                // 删除该元素后, 需要重新伸展树得到一个根节点
                // 从左子树中找到最大的节点(删除元素的前驱节点)作为新的根节点
                tree.left = topDownSplay(ele, tree.left);
                // 此时左子树不存在右儿子, 将原树的右子树直接赋给伸展后的左子树的右儿子
                tree.left.right = tree.right;
                tree = tree.left;
            }else {
                tree = tree.right;
            }
        }
        return tree;
    }
    /**
     * 伸展
     * @param ele
     * @return
     */
    public SplayNode<T> splay(T ele){
        return topDownSplay(ele, root);
    }
    /**
     * 自顶向下伸展
     * 构建两棵临时的树──左树和右树。没有被移走的节点构成的树称作中树。
     * 1、目标节点和root相连时：一次link操作完成伸展
     * 2、目标节点有父节点和祖先节点, 并且呈之字形：通过两次link操作完成伸展
     * 3、目标节点有父节点和祖先节点, 并且呈一字形：先通过一次旋转, 再通过一次link操作完成伸展 (这里不是很懂，如果也通过两次link操作也能达到把目标节点移动到root的目的啊????)
     * 注意此处的节点N, 最后所有的左树集中在N的右子树上, 而所有的右树集中在N的左子树上。
     * 因为每次left link需要将中树上的部分节点移到左树的最右端(也就是最大的位置上), 这里的节点l的作用可以看做是为了方便在左树的最右端继续添加从中树移过来的节点;
     * 同理, right link时, 节点r和节点l的作用类似。
     * @param ele
     * @param tree
     * @return
     */
    private SplayNode<T> topDownSplay(T ele, SplayNode<T> tree){
        if (tree == null){
            return null;
        }
        SplayNode<T> N = new SplayNode<T>();
        SplayNode<T> l = N;
        SplayNode<T> r = N;
        SplayNode<T> c;
        for (;;){
            int cmpResult = ele.compareTo(tree.element);
            if (cmpResult < 0){
                if (tree.left == null){
                    break;
                }
                /* rotate right*/
                if (ele.compareTo(tree.left.element) < 0){
                    c = tree.left;
                    tree.left = c.right;
                    c.right = tree;
                    tree = c;
                    if (tree.left == null){
                        break;
                    }
                }
                /* link right */
                r.left = tree;
                r = tree;
                tree = tree.left;
            }else if (cmpResult > 0){
                if (tree.right == null){
                    break;
                }
                /* rotate left */
                if (ele.compareTo(tree.right.element) > 0){
                    c = tree.right;
                    tree.right = c.left;
                    c.left = tree;
                    tree = c;
                    if (tree.right == null){
                        break;
                    }
                }
                /* link left */
                l.right = tree;
                l = tree;
                tree = tree.right;
            }else {
                break;
            }
        }
        /* assemble */
        l.right = tree.left;
        r.left = tree.right;
        tree.left = N.right;
        tree.right = N.left;
        return tree;
    }
    public void print(){
        if (root != null){
            print(root, root.element, 0);
        }
    }
    /**
     * @param node 打印的节点
     * @param ele ele 父节点的值
     * @param direction 0:根节点;-1:父节点的左儿子节点;1:父节点的右儿子节点
     */
    private void print(SplayNode<T> node, T ele, int direction){
        if (node != null){
            if (direction == 0){
                System.out.printf("%s是根节点\n", ele);
            }else {
                System.out.printf("%s是%s的%s儿子节点\n", node.element, ele, direction==-1?"left":"right");
            }
            print(node.left, node.element, -1);
            print(node.right, node.element, 1);
        }
    }
}

感谢:http://www.cnblogs.com/skywang12345/p/3604286.html
   http://www.cnblogs.com/UnGeek/archive/2013/04/10/3013333.html