介绍
2-3树是一种平衡二叉树,其目标是为了优化二叉搜索树,防止极端情况下时间复杂度的退化。
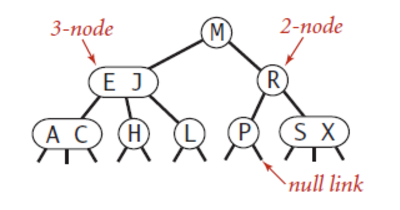
2-节点:含有一个键(及其对应的值)和两条链接,左链接指向的2-3树中的键都小于该结点,右链接指向的2-3树中的键都大于该结点。
3-节点:含有两个键(及其对应的值)和三条链接,左链接指向的2-3树中的键都小于该结点,左链接指向的2-3树中的键都小于该结点,中链接指向的2-3树中的键都位于该结点的两个键之间,右链接指向的2-3树中的键都待遇该结点。
为了保持树的平衡性,我们将会利用4-节点来在插入和删除过程中保持树的完美平衡。
将指向一棵空树的链接成为空链接。
一棵完美平衡的2-3查找树中的所有空链接到根节点的距离应该是相同的。
性质:
1. 一个节点包含一个或两个键值;
2. 每个内部节点有两个或三个子节点;
3. 所有子节点都在树结构的同一层,因此树的高度总是平衡的。
优势:
和标准二叉树由上向下生长不同,2-3树是由下向上生长的。在一棵大小为N的2-3树中,查找和插入操作访问的节点必然不超过$\log{N}$。
插入
2-3树之所以完美平衡,关键在于插入时的维护。涉及到2-节点、3-节点以及4-节点之间如何转换。
节点合并
与二叉查找树一样,我们将会在2-3树中找到一个合适位置来插入它,这个位置一定在树的底部。在插入前,我们可以保证这棵2-3树是完美平衡的(空树也是如此)。在底部插入一个节点后,就会导致底部“多出”一个节点,导致2-3树不完美平衡。
解决方案就是节点结合:包括将2节点转换为3节点,3节点转换为4节点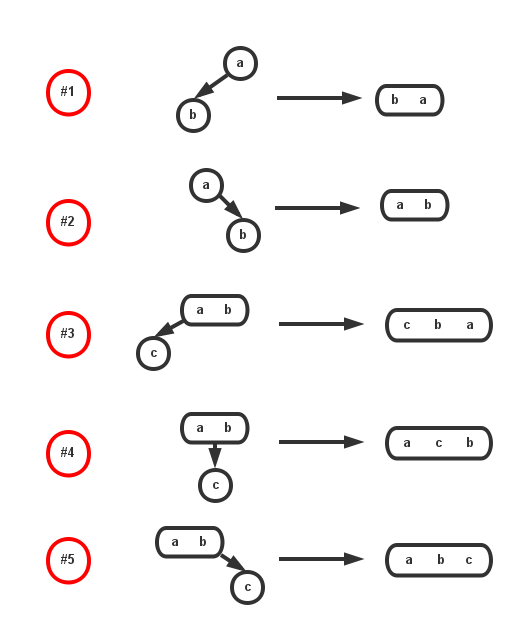
节点分裂
在上面的节点合并的操作中,出现了4-节点。然而4-节点是不能出现在最后的2-3树中的。因此我们需要将4-节点“肢解”,以确保这是一棵2-3树。
通常情况下,一个4-节点可以分裂成3个2-节点: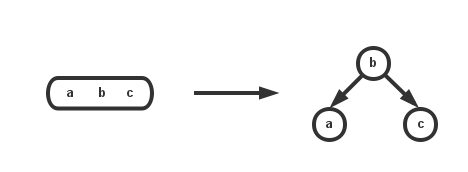
分裂的过程十分简单,只需要将4-叉节点从中间分开,并将中间的两个儿子分别重新接在a的右儿子和c的左儿子即可。
分解根节点
如果从插入节点到根节点的路径上全都是3-节点,所以根节点最终变成一个临时的4-节点。此时按照上述的分解后,整棵树的高度增加1,保证了2-3树的完美平衡。
删除
2-3树的插入操作是有点复杂的,然而删除操作更加麻烦。
2-3树在实际中很少使用,由于其需要大量的节点变换(从2-节点到3-节点到4-节点甚至到5-节点),这些变换在实际代码中是很复杂的,所以现在几乎没有2-3树的具体实现。
感谢: https://riteme.github.io/blog/2016-3-12/2-3-tree-and-red-black-tree.html#_5