数据结构与算法(9): 树形结构- 红黑树

发表于   |   分类于

介绍

  红黑二叉查找树（红黑树）：基本思想是用标准的二叉查找树（完全由2-节点构成）和一些额外的信息（替换3-节点）来表示2-3树。
  红链接：将两个2-节点连接起来构成一个3-节点。
  黑链接：是2-3树中的普通链接。

红黑树另一种定义是含有红黑链接并满足下列条件的二叉查找树：

  1. 红黑树是二叉查找树
  2. 根节点必须为黑色（根节点没有父节点）
  3. 红链接均为左链接
    将红链接统一在一个方向是为了方便其它操作。如果不统一，3-节点就有两种情况，4-节点就有5中情况，非常不利于我们判定当前是什么节点。并且，对于右边的红链接，我们可以通过二叉搜索树的旋转操作来将其变为左链接。具体的会在之后解释。
  4. 没有任何一个节点同时有两条红链接相连
    因为连续的2个红链接表示的是4-节点。当然，跟2-3树一样，插入/删除的过程中还是允许临时的4-节点。
  5. 空节点（NULL/None）为黑色。这样方便将方便识别没有儿子的2-节点。
  6. 该树是完美黑色平衡的，即任意空链接到根节点的路径上的黑链接数量相同。

颜色表示，为了方便做出以下规定：
  1. 根节点为黑色；
  2. 空节点为黑色。

操作

旋转

  在进行某些操作中可能会出现红色右链接或者两条连续的红链接，但在操作完成前都可以通过旋转来修复。红黑树的旋转只有两种：顺时针旋转（右旋转）和逆时针旋转（左旋转）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
    * 左旋转：红色右链接 -> 红色左链接
    *
    * @param node
    * @return
    */
   private Node<T> rotateToLeft(Node<T> node) {
       Node<T> x = node.right;
       node.right = x.left;
       x.left = node;
       x.color = node.color;
       node.color = RED;
       return x;
   }
   
   /**
    * 右旋转： 红色左链接 -> 红色右链接
    *
    * @param node
    * @return
    */
   private Node<T> rotateToRight(Node<T> node) {
       Node<T> x = node.left;
       node.left = x.right;
       x.right = node;
       x.color = node.color;
       node.color = RED;
       return x;
   }

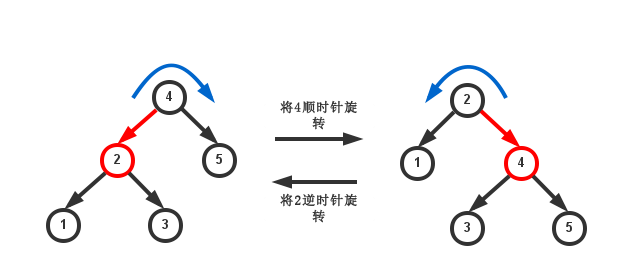
插入

  在2-3树中，我们将新插入的节点与树的底部节点合并，然后再做调整。为了表示合并，我们将新插入的节点均设为红色，表示与底部节点相连接。然而插入后，新的红节点可能会违反我们的规定，因此需要在回溯的时候进行调整。

  1. 情况一：红色右链接
      当我们发现某个节点的左儿子是黑色但右儿子是红色时，我们要将右边的红色链接转到左边来。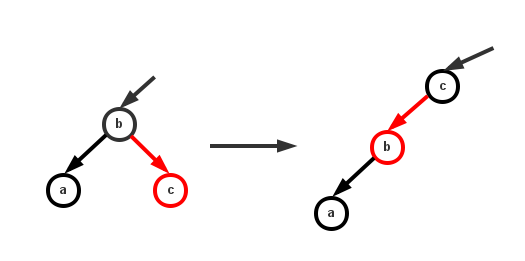

  2. 情况二：分解4-节点
      当左儿子和右儿子都是红色时，就代表着一个4-节点，为此我们可以直接将其反色来分解它。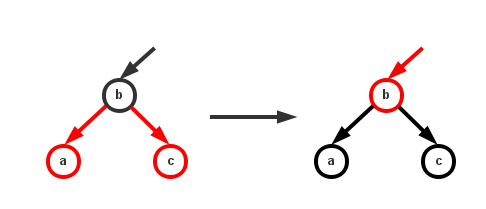

  3. 情况三：连续红色左链接
      当出现连续的红色左链接时，需要经过一次右旋转变成一个4-节点，再进行一次反色分解它。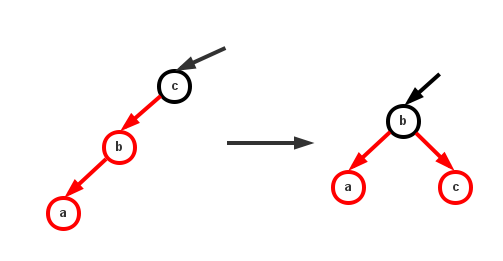

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
    * 插入实现
    */
private Node<T> insert(T ele, Node<T> tree){
       if (tree == null){
           return new Node<>(ele, RED);
       }
       int cmpResult = ele.compareTo(tree.element);
       if (cmpResult < 0){
           tree.left = insert(ele, tree.left);
       }else if (cmpResult > 0){
           tree.right = insert(ele, tree.right);
       }else {
           // duplicate; do nothing
       }
       // check balance
       if (isRed(tree.right) && !isRed(tree.left)){
           // 情况一：红色右链接
           tree = rotateToLeft(tree);
       }
       if (isRed(tree.left) && isRed(tree.left.left)){ // 该步在下一步flipColors之前进行校验
           // 情况三：连续红色左节点, 进行一次右旋转变成情况二4-节点
           tree = rotateToRight(tree);
       }
       if (isRed(tree.left) && isRed(tree.right)){
           // 情况二：分解4-节点
           tree = filpColors(tree);
       }
       return tree;
   }

红黑树和AVL比较

AVL是严格的平衡树，红黑树是非严格的平衡树。

  1. 两者在删除和插入的时间复杂度一致，都为$O(\log{n})$。
  2. 两者在插入时的旋转调整复杂度都是$O(1)$。
  3. 在删除之后旋转调整，AVL的复杂度在$O(\log{n})$,即多次旋转，一直检查到根节点的平衡。而红黑树调整的级别在$O(1)$，因为其能保证在三次旋转之内达到稳定。
  4. 因为树的高度的关系，红黑树适用于插入删除频繁，AVL树适用于查找频繁。但其实红黑树应用比AVL广很多。

感谢:https://riteme.github.io/blog/2016-3-12/2-3-tree-and-red-black-tree.html#_5