定义
给定n个权值作为n个叶子结点,构造一棵二叉树,若树的带权路径长度达到最小,则这棵树被称为哈夫曼树。
- 路径和路径长度
在一棵树中,从一个结点往下可以达到的孩子或孙子结点之间的通路,称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1,则从根结点到第L层结点的路径长度为L-1。
- 节点的权及带权路径长度
若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积。
- 树的带权路径长度
树的带权路径长度规定为所有叶子结点的带权路径长度之和,记为WPL。
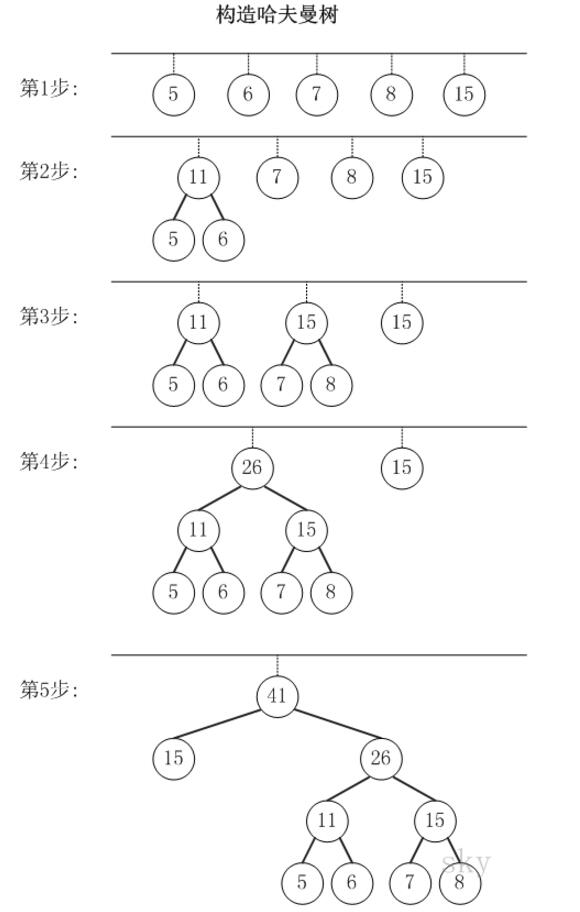
构造规则
假设有n个权值,则构造出的哈夫曼树有n个叶子结点, n个权值分别设为 w1、w2、…、wn。哈夫曼树的构造规则为:
- 将w1、w2、…,wn看成是有n 棵树的森林(每棵树仅有一个结点);
- 在森林中选出根结点的权值最小的两棵树进行合并,作为一棵新树的左、右子树,且新树的根结点权值为其左、右子树根结点权值之和;
- 从森林中删除选取的两棵树,并将新树加入森林;
- 重复2~3步,直到森林中只剩一棵树为止,该树即为所求得的哈夫曼树。